遺伝的アルゴリズム
(GA : Genetic Algorithms)
まえがき
遺伝的アルゴリズムは現在,最も注目を浴びている分野の一つである.
地球上に生物が30数億年前にはじめて誕生してから,今日までの長い期間をかけて
進化した結果,遂に人類にまでたどり着いたみられている.
その進化の基礎をなすのが遺伝機構である.
親から子に遺伝情報が伝えられる過程において,交叉や突然変異など
の遺伝操作を経て新しい遺伝子の組み合わせを生じ,その結果生まれた子孫が
適者生存という,環境への適合性を評価されて進化してきたものとみられている.
GAはこのような機能をコンピュータソフトに取り入れて各種問題解決に活用することを
狙っている.
20数年前に米国ミシガン大学ホランド博士により提案されてから,多くの
研究者により研究されてきた.モデル化が困難な問題にも適用でき,
かつ比較的簡単なアルゴリズムながら優れた性能を持っていることから,
適用分野が広がってきている.
以下の2種類のGAについて簡単に説明する.
シンプルGA
GAのうちシンプルGA(SGA)といわれる最も基本的な方式について説明する.
 右図に簡単な系統を示す.
右図に簡単な系統を示す.
まず所定数の個体からなる集団を用意する.
各個体の遺伝子表現はビットストリングとする.
一つの世代の動作は最初に集団から
2個の個体を選択し,これをメイティングプールに入れる.
ここでは2個体の間で交叉,
突然変異からなる遺伝子操作が行なわれ,
その結果得られた新しい2個の個体を新集団にいれる.
この操作を人口(集団の個体数)分だけ実施すると新集団を元の
集団に移す.この動作を所定の世代数だけ実行して終了する.
以上の操作の内,選択操作では各個体の適合値
の高いものを高い確率で選び出すようになっている.
各個体の従って目的とする最適状態で
最大の適合値なるように適合関数を設計しておけば,世代の進行に応じて
最適状態に近づくことになる.
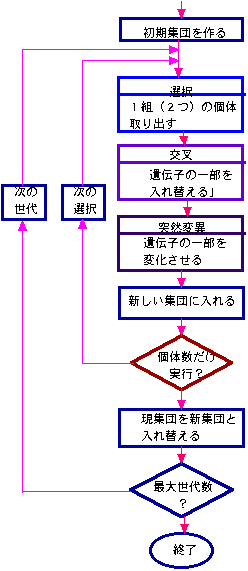
以上の操作をフローチャートに示すと下図のようになる.
トップに戻る
- 遺伝子表現
- 解くべき問題に応じてそれを遺伝子で表現する必要がある.遺伝子の表わし方
には通常はビットストリングを使用する.問題によっては整数や実数などが
使用される.こうして表わした遺伝子の集合として染色体を設ける.
なお初期集団の遺伝子の値は通常は一様乱数を用いて確率的に決める.
- 適合関数及び適合値
- 自然界における適者生存の原理を適用するため,適者の程度をを表わすものとして
適合関数(fitness function)を使用する.
適合関数は遺伝子表現を基に目的状態になった時,その値が最大になるように決める.
適合関数より求めた値が適合値となる.
- 選択(selection)
- 次世代に残すものを選び出す作業であり,確率的に行なわれる.
各個体の適合値に比例した確率で個体が取り出されるようになっている.
このような方式をルーレットホイール方式という.ルーレットでは玉の
入る確率がその面積に比例するようになっていることから命名された.これにより
適合値の高い個体がより高い頻度で取り出されることになる.
- 交叉(crossover)
- 交叉は2個の個体間で遺伝子を交換する操作であり,
SGA では通常1点交叉が行なわれる.1点交叉では2個の遺伝子間で任意に選んだ
1個の交叉点の前方と後方で互いに入れ換えて新しい遺伝子を生成する.
交叉点の位置の選定は一様分布の確率により行なう.
- 突然変異(mutation)
- 突然変異は各個体の遺伝子の値を確率的に変更する操作である.
通常は交叉と同時に行なわれ,遺伝子の各ビットを端から順に走査しつつ,
所定の確率に従ってビット値を変化させる.その目的は新しい個体を作るにあるが,
ローカルミニマムに陥ったときに,そこから抜け出すのに効果的である.
トップに戻る
GAにおける遺伝子表現は生物におけるDNAとは異なり,人工物であるので任意に設定する
ことができる.その代表的な1つが順序表現である.
例えばセールスマン巡回問題(TSP)を解くための表現としては1から都市の数までの整数の順列を採用することができる.このような整数の順列を採用した場合,遺伝子操作方法がバイナリビット表現とは異なってくる.特に大きく変わるのが交叉方法であり,
これまで各種の方法が検討されてきた.その代表的な方法について
順序問題へのGAの適用および
順序型GAの遺伝子表現と操作(PDF判)にて説明している.
トップに戻る
小野 俊彦 (Toshihiko Ono)
 右図に簡単な系統を示す.
右図に簡単な系統を示す.